Nos tracteurs en 2035 et le pompage-turbinage thermique.
La fin des moteurs thermique est programmée pour 2035. On peut se demander comment les tracteurs agricoles rouleront alors. Personne n'en parle actuellement (2023). Pourtant, 2035, c'est dans 12 ans. On y sera vite. Il est probable que les tracteurs seront électriques. Les fermes laitières ont également besoin d'électricité pour traire. De nombreux fermiers disposent de très grands toits recouverts de panneaux photovoltaïques. Ils disposent donc d'une énergie gratuite mais intermittente. Certains jours, ils ne pourront donc pas travailler ou bien les vaches ne seront pas traites. Impensable. Il faut donc pouvoir stocker l'électricité. Une solution souvent proposée est l'hydrogène mais qui a un très mauvais rendement : pour produire l'hydrogène, il faut le fabriquer par électrolyse. Cela a un rendement de 70 %. L'hydrogène produit est alors très léger et prend beaucoup de volume. Il faut donc le comprimer. Mais cela produit de la chaleur comme dans une pompe à vélo. Encore de la perte. Quand on a l'hydrogène, il faut pouvoir le valoriser. Si cela se fait dans une pile à combustible, celle-ci a un rendement de 50 %. Au total, on perd les trois-quarts de l'énergie. Il faut donc s'attendre à un prix assez élevé pour l'hydrogène.
Heureusement, il y a une meilleure solution : la batterie de Carnot avec pompe à chaleur. Ce dernier terme a son importance, car il existe d'autres batteries de Carnot, sans pompe à chaleur, où on se contente de stocker l'électricité sous forme de chaleur, mais qui ont un rendement moindre, semblable à celui des turbines de centrales nucléaires, puisque fonctionnant selon le même principe,
On peut décrire cette batterie de Carnot de la façon suivante. Un moteur thermique exploite toujours une différence de température. Dans la batterie de Carnot avec pompe à chaleur, deux réservoirs sont la source chaude et la source froide d'un moteur à combustion externe (souvent un moteur Stirling) qui va entraîner un alternateur pour faire de l'électricité lors du déstockage. Pour stocker l'électricité, une pompe à chaleur extrait la chaleur du réservoir froid et ajoute à cette chaleur extraite la chaleur venant du travail du compresseur de la pompe à chaleur, comme le font toutes les pompes à chaleur ou les frigos, le tout servant à chauffer le réservoir chaud. Le compresseur est alimenté par l'électricité des éoliennes ou des panneaux solaires. Le travail de compression représente donc l'énergie à stocker. Lorsqu'on veut récupérer l'électricité, le froid qui sert à refroidir le moteur est celui qu'on a créé avec la pompe à chaleur. La chaleur qui a été retirée n'est pas perdue : elle se trouve dans le réservoir chaud où se trouve également la chaleur du compresseur. Quand le réservoir froid refroidit le moteur pour qu'il produise de l'électricité, il soustrait sa chaleur du réservoir chaud et il reste donc dans celui-ci l'équivalent de l'énergie stockée qui va devenir le travail moteur. Le moteur devrait donc restituer exactement et entièrement l'électricité qui a été stockée, puisqu'il ne faut pas fournir l'énergie qu'on ne perd pas. L'électricité qu'il faut fournir est uniquement celle qui doit être stockée.
Dit plus simplement : un congélateur extrait la chaleur d'un réservoir qui devient très froid pour la mettre dans un autre réservoir qui devient très chaud. Pour refaire de l'électricité, cette différence de température est appliquée à un moteur thermique (moteur Stirling ou turbine) mais sans qu'il faille apporter de l'extérieur la chaleur qu'on arrache au moteur. En fait, il s'agit d'un pompage-turbinage thermique, comme dans les STEP, avec un niveau inférieur qui est pompé dans le niveau supérieur pendant le stockage, pour être ensuite déversé dans le niveau inférieur pour récupérer l'énergie.
On peut aussi exprimer cela de la façon suivante : lors du stockage, un congélateur crée une différence de température entre deux réservoirs thermiques, pompant la chaleur de l'un dans l'autre. Lorsqu'on veut récupérer l'électricité, cette différence de température est appliquée à un moteur à combustion externe. En refroidissant le moteur, le réservoir froid récupère la chaleur qu'il avait cédée au réservoir chaud lors du stockage. Cette chaleur ne quittant jamais les réservoirs, elle ne doit pas être apportée, contrairement à ce qui se passe dans une centrale nucléaire où beaucoup de chaleur est évacuée et donc perdue dans l'atmosphère via les cheminées hyperboliques. La seule énergie qu'il faut apporter dans notre batterie de Carnot est l'électricité à stocker, qui est fournie par les panneaux solaires, et c'est la seule qui sortira de la batterie. Cette électricité sera donc intégralement restituée lors du déstockage. Le rendement théorique de cette batterie est donc de 100 % comme expliqué également dans https://onlinelibrary.wiley.com/doi/full/10.1002/ente.201900895 .
Jusqu'à présent, j'avais considéré la batterie de Carnot avec pompe à chaleur sous une forme idéale, où le compresseur nécessite le même travail pour stocker l'électricité que le travail fourni par le moteur à combustion externe lors de la décharge. Or, il n'en est rien en réalité. https://onlinelibrary.wiley.com/doi/full/10.1002/ente.201900895 explique que le rendement aller-retour est en fait de 45 % et non de 100 % comme une machine idéale le permettrait, du fait des imperfections des compresseurs et des moteurs. Ci-dessous, je fais un petit calcul pour dire ce que devient notre batterie.
Il ne faut pas confondre le rendement de la batterie de Carnot avec pompe à chaleur, qu'il vaut mieux appeler efficacité aller-retour, avec le rendement de Carnot de la turbine. Dans un système comme celui d'Azelio (Suède, mais en faillite actuellement) qui consistait à chauffer de l'aluminium à 600 °C avec des résistances électriques alimentées par les panneaux solaires pour ensuite actionner une turbine à vapeur tout à fait classique refroidie par aéroréfrigérant, le rendement de la batterie se confond effectivement avec le rendement de la turbine. Mais avec le pompage turbinage thermique, il n'en va pas de même. Pour le comprendre, il faut examiner les diagrammes T,s (température Kelvin, entropie) du compresseur et de la turbine. Je dessine très mal. Voici ce que cela donne.
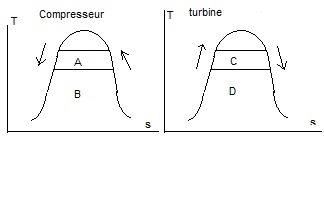
Le travail du compresseur est A tandis que B est ce que la pompe à chaleur extrait comme calories du réservoir froid. Le travail de la turbine est C et il faut retirer la quantité de chaleur D de la turbine et D retourne dans le réservoir froid. L'électricité stockée venant des panneaux solaires est A.
A doit donc être le plus grand possible, tandis que B doit être la plus petite possible, afin que le réservoir froid soit le plus petit possible pour qu'il soit moins coûteux. C'est exactement le contraire des pompes à chaleur dans nos maisons, qui doivent consommer le moins possible et donc avoir A très petit alors que B, la chaleur prélevée gratuitement dans l'air, doit être la plus grande possible.
Dans la batterie de Carnot avec pompe à chaleur idéale, donc de façon théorique, A et C sont identiques d'une part, et d'autre part B et D sont également identiques. Le rendement de Carnot de la turbine C / (C + D) n'intervient pas dans ces égalités. Si le milieu de stockage est de l'eau entre 70°C et 95 °C, le rendement théorique de la turbine est de 23 %, alors que l'efficacité aller-retour théorique de la batterie de Carnot est de 100 %.
Malheureusement, la transformation de l'énergie calorifique en énergie mécanique et inversement n'est pas parfaite dans la turbine et le compresseur. Les aubes de ces machines ont des pertes. Nous avons donc un rendement isentropique qui affecte ces deux machines. Il est d'environ 70 %, ce qui conduit à une efficacité aller-retour de la batterie de 0,7 * 0, 7 = 50 %. Et ce, malgré que le rendement de Carnot de la turbine n'est que de 23 %. La perte de chaleur au travers des parois des réservoirs thermiques est de 10 %. Le rendement global de la batterie de Carnot avec pompe à chaleur est donc effectivement de 0,50 * 0,90, soit 45 %. D'autres sources parlent d'un rendement isentropique de 85 %. L'efficacité aller-retour de la batterie de Carnot avec pompe à chaleur serait alors de 65 %.
Le stockage de chaleur proposé par Azelio a comme inconvénient de nécessiter un aéroréfrigérant. Celui-ci peut causer la légionellose, ce qui est impossible avec la batterie de Carnot avec pompe à chaleur, puisque le refroidissement de la turbine se fait en circuit fermé et ne peut donc pas contaminer l'extérieur, contrairement à un aéroréfrigérant qui charge l'air ambiant de vapeurs suspectes.
La pompe à chaleur travaille à une température beaucoup plus élevée que les pompes à chaleur dans nos maisons. La température est un facteur limitant comme il est dit dans le texte suivant : "Avec les compresseurs à vis, la température de l'air comprimé varie entre + 70 et + 80°C et, avec les compresseurs à piston, elle varie entre + 150 et + 160°C" notamment pour des raisons de lubrification. Pourtant, il doit être possible de monter nettement plus haut en température pour avoir un meilleur rendement du moteur et des réservoirs plus petits et moins chers, puisque Airthium https://airthium.com/our_heat_pump présente une pompe à chaleur montant à 500 °C. On pourrait aussi avoir recours à la réfrigération magnétique que vous pouvez découvrir dans https://fr.wikipedia.org/wiki/R%C3%A9frig%C3%A9ration_magn%C3%A9tique Une entreprise développe cette technique : https://magnoric.com/fr/ . Un autre constructeur https://www.equium.fr/ propose une pompe à chaleur acoustique.
Enogia, une entreprise de Marseille : https://enogia.com/orc/ fabrique des compresseurs pouvant atteindre 600 °C.
Dans le même genre, j'ai trouvé Climeon https://climeon.com/power-stations/
Les séchoirs en grange sont une excellente technique pour faire du foin,mais malheureusement, il faut bien reconnaître que cela a son prix. Et que, contrairement à ce que disent les constructeurs, le procédé est énergivore. Cette technique est excellente parce que, le préfané est encore humide quand on le place. A ce stade, il n'y a donc pas de pertes de feuilles, Ensuite, on n'y touche plus, et on conserve donc toutes les feuilles, la partie la plus nourrissante du fourrage, ainsi qu'une couleur bien verte. C'est pour cela que j'ai pensé coupler une batterie de Carnot avec pompe à chaleur alimentée par des panneaux solaires à un séchoir AgriCompact qui est moins coûteux qu'un séchoir en grange où le fourrage est entreposé dans des cellules qui montent à 7 m de haut.
Stocker l'électricité de panneaux solaires dans une batterie de Carnot avec pompe à chaleur devrait pouvoir fournir de l'électricité jour et nuit pendant deux semaines. Le mazout utilisé actuellement dans le séchoir AgriCompact est remplacé par l'électricité. Ce séchoir de 24 ballots peut sécher 1.000 ballots par an, soit 200 tonnes de foin. Dans sa version actuelle, il utilise 6 litres de mazout pour sécher un ballot rond de 200 kg, soit 6.000 litres de fuel par an. Le chauffage de l'air utilise 3 litres de mazout par ballot. Chauffer l'air de séchage avec de l'électricité utilisera la même quantité d'énergie, et comme un kg de mazout produit 10 kWh, nous aurons besoin de 30 kWh/ballot d'électricité. Par contre, le moteur à explosion qui doit entraîner le ventilateur utilise également 3 litres/ballot, mais ce moteur a un rendement de 25 %. Avec un moteur électrique, le rendement est proche de 100 % et seulement 0,25 * 3 kg mazout * 10 kWh/kg mazout = 7,5 kWh/ballot seront nécessaires pour faire tourner le ventilateur. Au total, on aurait besoin de 37,5 kWh * 1.000 ballots = 37.500 kWh/an.
Si on veut que la batterie de Carnot contienne suffisamment d'énergie pour sécher pendant 16 jours et que ce séchoir a besoin de 4 jours pour sécher 24 ballots, cela signifie qu'il faut stocker 16 jours / 4 jours par séchage * 24 ballots/séchage * 37,5 kWh/ballot = 3.600 kWh.
Enogia https://enogia.com/orc/ propose des micro-turbines dont la gamme de puissance s'étend entre 10 kW et 180 kW, exactement ce qu'il faut dans nos fermes. J'ai l'impression qu'une aussi petite turbine peut se mettre en marche et être arrêtée rapidement, puisque dans une petite machine, les dilatations doivent être réduites, contrairement à ce qui se passe avec les grandes turbines de centrales nucléaires qui nécessitent un démarrage graduel.
Une batterie de Carnot avec pompe à chaleur peut utiliser des sels fondus ou du basalte pour stocker la chaleur à 400 °C, mais il est possible également d'utiliser de l'eau sous 100 °C. Dans les deux exemples qui suivent, nous prendrons d'abord une batterie à 400 °C pour ensuite présenter une batterie avec de l'eau comme milieu de stockage.
1. Stockage à 400 °C
Prenons un réservoir chaud dont la température évolue de 250 °C à 450 °C. Dans le réservoir froid, nous aurons de la glace en fusion qui reste donc constamment à 0 °C. La température moyenne côté chaud est en fait (250 + 450) / 2 = 350 °C
Dès lors, le rendement de Carnot sera (350 - 0) / (350 + 273) = 0,56.puisque ce rendement théorique est donné par (Tchaud - Tfroid) / Tchaud, où T est la température en degrés Kelvin qui peut aussi s'exprimer par la température Celsius °C à laquelle on ajoute 273 °C.
Pour que la turbine reçoive toujours la même température afin de conserver un rendement constant, il faudrait utiliser 2 réservoirs chauds et 2 réservoirs froids, mais cela coûte évidemment le double. Avec un seul réservoir, la température décroît et le rendement devient de plus en plus mauvais. Nous pourrions conserver la température à l'entrée de la turbine constamment à 250 °C et l'alimenter par le réservoir dont la température décroît de 450 °C à 250 °C. Le rendement de la turbine est alors de 48 %.
La batterie doit pouvoir stocker 3.600 kWh. Le réservoir chaud contient cette chaleur, mais aussi celle qui sera arrachée à la turbine par le réservoir froid. Le rendement de 0,48 correspond à ces 3.600 kWh. Le froid correspond donc à 3.600 kWh / 0,48 * 0,52 = 3.900 kWh. Au total, le réservoir chaud devra stocker 3.600 + 3.900 = 7.500 kWh qui devront traverser la turbine..
Toutefois, la turbine a un rendement isentropique de 70 %. Le réservoir chaud devra en fait contenir 7.500 kWh * 100 / 70 = 10.714 kWh afin de compenser les pertes isentropiques dans la turbine. La perte dans la turbine est donc de 10.714 - 7.500 = 3.214 kWh.
Cette perte devra être fournie par les panneaux solaires en plus des 3.600 kWh à stocker. D'autre part, la pompe à chaleur perd également 3.214 kWh directement pendant le stockage. Ceux-ci devront également être fournis par les panneaux solaires mais seront directement dissipés dans le compresseur. Il ne faudra donc pas les stocker dans le réservoir chaud. Au total, les panneaux solaires devront fournir 3.600 kWh à stocker + 3.214 kWh perdus dans la turbine + 3.214 kWh perdus dans la pompe à chaleur = 10.028 kWh. Si ces 10.028 kWh doivent être fournis en 15 jours par des panneaux photovoltaïques et que ces panneaux produisent 1 kWh /jour et par m², 668 m² de panneaux seront nécessaires. Si le réservoir est plein en 25 jours, 400 m² de panneaux solaires suffisent.
La pompe à chaleur reçoit 10.028 kWh des panneaux solaires et les ajoute aux 3.900 kWh qui seront pompés depuis le réservoir froid dans le réservoir chaud, mais perd 3.214 kWh qui n'atteindront pas le réservoir chaud. Finalement, le réservoir chaud reçoit 10.028 + 3.900 - 3.214 = 10.714 kWh.
Si le réservoir chaud contient du basalte dont la chaleur spécifique est la moitié de celle de l'eau, son volume sera 10.714 kWh / 0,5 chaleur spécifique / 1.000 kg/m³ / (450 °C - 250 °C) * 860 kcal/kWh = 92 m³, soit 4,5 m * 4,5* 4,5. Sa surface sera 4,5 * 4,5 * 6 = 122 m².
On voit souvent des réservoirs thermiques très élancés, beaucoup plus hauts que larges. C'est une erreur, car le cube est le prisme dont la surface de déperdition est la plus petite par rapport à son volume.
L'Université de Bordeaux fait des recherches sur les batteries thermiques comme vous pouvez le voir dans https://www.youtube.com/watch?v=BFhHS4EWcBE&t=361s , et cela pourrait conduire à un réservoir chaud 4 fois plus petit, et donc moins cher.
Le réservoir froid contient de l'eau pure à 0 °C qui passe de l'état liquide à l'état solide. Il reste donc constamment à 0°C.. Pour fondre de la glace, 80 kcal sont nécessaires par kg. En congelant de l'eau à 0 °C, mais en restant à 0 °C, on peut stocker 80 kcal/ kg * 1.000 kg/m³/ 860 kcal/kWh = 93 kWh/m³.
La conductivité thermique de l'eau à 0 °C est 0,55 tandis que celle de la glace à la même température est de 2,1. Nous voyons donc que la glace conduit mieux la chaleur que l'eau. Il faudra probablement récupérer cette chaleur en plaçant des serpentins tout comme dans le basalte du réservoir chaud.
Le réservoir froid doit céder 3.900 kWh. Son volume sera 3.900 kWh / 93 kWh/m³ = 42 m³, soit 3,5 m * 3,5 * 3,5. et sa surface 3,5 * 3,5 * 6 = 74 m².
Pour résumer :
D'abord le stockage :
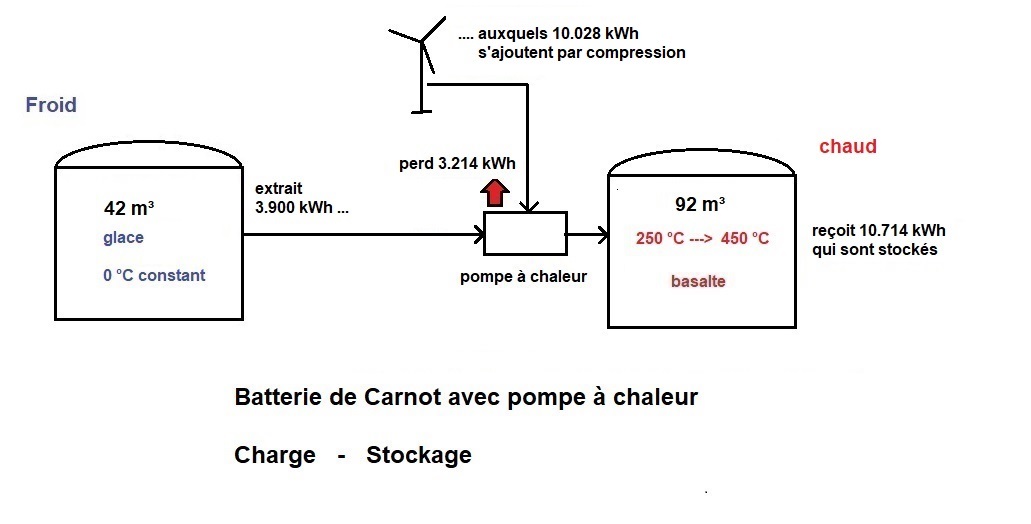
Ensuite, la récupération de l'électricité (déstockage) :
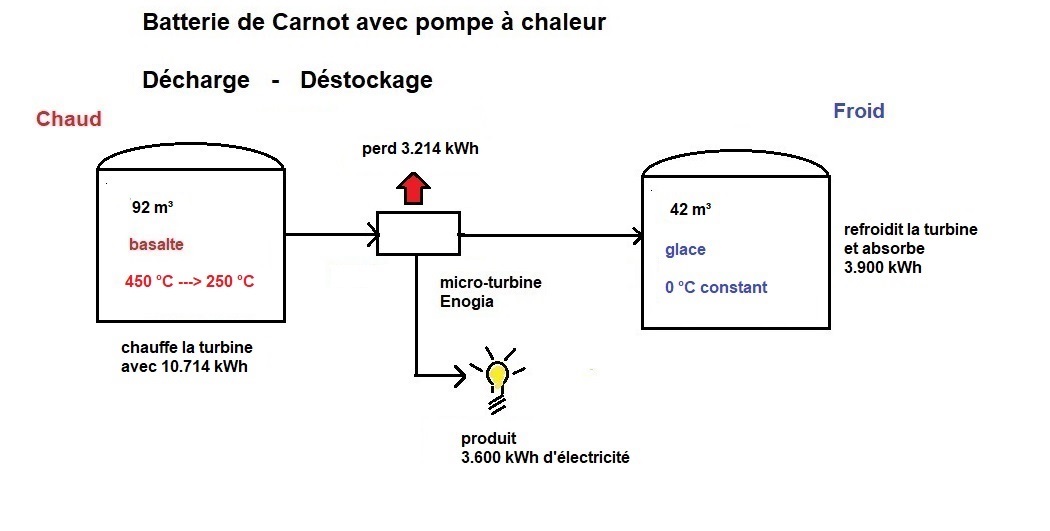
Pour connaître les déperditions de chaleur, nous utilisons la formule :
Déperdition = surface du réservoir * différence de température avec l'extérieur / épaisseur de l'isolant * coefficient laine de roche * durée
Déperdition en un mois du réservoir chaud = 122 m² * (450 °C+ 250 °C ) / 2 / 1 m épaisseur isolant * 0,04 coefficient laine de roche * 30 jours * 24 heures / 860 kcal/kWh = 1.430 kWh, soit 1.430 / 10.714 = 13 % perdus en un mois. On voit donc que la batterie de Carnot avec pompe à chaleur peut conserver l'énergie pendant plusieurs mois. C'est la conséquence de la taille du réservoir. Au plus les réservoirs sont grands, au moins ils perdent de chaleur en comparaison avec l'énergie qu'ils contiennent. Cela vient du fait que la surface de déperdition de la chaleur dans un cube est le carré du côté, tandis que le volume, et donc la quantité de chaleur conservée, augmente avec son cube.
Le séchoir en grange que je prends comme exemple est un AgriCompact de 24 ballots qui, s'il fonctionne totalement à l'électricité, demande 37 kWh/ ballot, comprenant la ventilation et le chauffage de l'air. Si le foin est sec en deux jours, 37 kWh/ballots * 24 ballots / 48 heures sera la puissance nécessaire pour la turbine, soit 18,5 kW. Dans une batterie de Carnot avec pompe à chaleur idéale, l'énergie produite par la turbine est la même que celle consommée par le compresseur de la pompe à chaleur. Celle-ci devrait donc être de 18,5 kWh par jour * 100 /70 en tenant compte d'un rendement isentropique de 70 %, soit 26 kWh. Ce devrait être la puissance de la pompe à chaleur.
Généralement, les réservoirs en acier sont cylindriques. Pour la facilité, je les prends cubiques. Si le réservoir chaud est fait en acier d'une épaisseur de 15 mm, le prix de l'acier serait : 122 m² * 0,015 m * 7.000 kg/m³ * 1,5 €/kg = 20.000 €. Il sera isolé avec de la laine de roche d'une épaisseur de 1 mètre. La laine de roche coûte 320 €/m³. Cette isolation devrait donc coûter 122 m² * 1 m * 320 €/m³ = 39.000 €. Il faut ajouter ce que les réservoirs contiennent. Le basalte coûte 85 € la tonne et et son poids spécifique est de 2,7 à 3 kg/dm³. Un mètre cube de basalte pèse 3 tonnes et 92 m³ coûtent 3 T/m³ * 92 m³ * 85 €/T = 23.500 €. En tout, les matériaux du réservoir chaud coûtent 82.500 €.
S'il est fait en béton, le réservoir froid coûtera 42 m² * 0,20 m épaisseur béton * 500 €/m³ béton mis en place = 4.200 €. Son isolation en paille coûte 20 €/m³. Elle coûte donc 42 m² * 0,50 m épaisseur * 20 €/m³ = 420 €. L'eau dans le réservoir froid coûtera 42 m³ * 5 €/m³ = 210 €
La petite turbine d'Enogia https://enogia.com/orc/ de 10 kW coûte 40.000 €, Prenons 40.000 € pour la pompe à chaleur de 30 kW, alors qu'une pompe à chaleur géothermique de 18 kW pour chauffer nos maisons coûte 13.000 € TVA comprise. Au total, les matériaux coûteraient donc 164.000 €, auxquels il faut ajouter la main d'oeuvre et le bénéfice du patron, sans oublier les serpentins, soit 230.000 € pour la batterie. Si nous ajoutons 230.000 € pour la batterie aux 140.000 € pour un séchoir AgriCompact de 24 ballots permettant de sécher 1.000 ballots par an ou 200 tonnes, ainsi que 400 m² de panneaux solaires à 300 €/m² = 120.000 €, cela fait un total de 490.000 €. Le gain annuel en gasoil sera de 6 litre/ballot * 1.000 ballots *1 €/litre gasoil = 6.000 € épargnés par an.
Il faudra probablement trouver un moyen d'équilibrer les pertes de chaleur dans les deux cuves, sinon, lorsqu'elles reçoivent l'énergie à stocker, l'eau chaude n'aura pas atteint sa température maximale quand la glace se sera complètement solidifiée, puisque l'écart de température du réservoir chaud avec l'extérieur est beaucoup plus important et que cela provoque un refroidissement supplémentaire du réservoir chaud. A chaque cycle de stockage, cela va se représenter et finalement la température du basalte sera de plus en plus basse. Une possibilité est de chauffer le basalte avec des résistances électriques alimentées par les panneaux solaires quand la glace est presque totalement solidifiée, c'est-à-dire quand sa température commence à descendre sous 0°C.
En reprenant l'exemple du séchoir en grange de 24 ballots, on pourrait se dire qu'il serait plus avantageux de produire l'électricité pour le ventilateur avec une plus petite batterie de Carnot (7,5 kWh/ballot), alors que réchauffer l'air peut se faire sans électricité, directement avec la chaleur contenue dans un réservoir thermique (30 kWh/ballot). En refaisant les calculs, nous obtenons pratiquement la même chose que le tout électrique, mais avec de nombreux désavantages : il est intéressant d'avoir une bonne réserve d'électricité en dehors de la saison de fenaison pour pouvoir faire fonctionner la salle de traite, le tracteur électrique, etc. D'autre part, le tout électrique demande un réservoir chaud beaucoup plus grand qu'avec le chauffage thermique de l'air du séchoir, ce qui est beaucoup plus favorable pour conserver la chaleur très longtemps, les grands réservoirs ayant moins de déperditions de chaleur que les petits.
Au lieu d'utiliser une micro-turbine, on pourrait également utiliser un moteur Stirling. Le moteur Stirling est réversible et peut devenir une pompe à chaleur pouvant générer des températures de -200 °C et monter jusque 700 °C. Ce moteur avait des problèmes d'étanchéité à faible frottement, mais ce défaut a été résolu par l'invention du moteur Stirling à piston libre. Trois entreprises s'occupent de sa fabrication :
Tous les fermiers n'auront pas besoin de 3.600 kWh de réserve. Nous avions déduit ce montant du fait de la présence sur la ferme d'un séchoir consommant 37.000 kWh en une saison, ce qui est très énergivore. Si ce séchoir est absent, par exemple si le foin peut être séché dans un hangar et que cette méthode s'avère efficace, le fermier pourrait se contenter d'une réserve d'électricité de 1.200 kWh, par exemple. Cela reste considérable, puisque cette énergie permet à une voiture électrique de rouler 600 km par jour pendant 10 jours consécutifs si elle consomme 20 kWh / 100 km.
Si le prix d'une batterie au lithium de 3.600 kWh est le même prix que celui d'une batterie domestique, ce serait 7.000 € pour 13 kWh. Notre batterie qui coûte 230.000 € en version thermique coûterait alors 3.600 kWh * 7.000 € / 13 kWh = 2 millions d'euros. Une batterie au lithium de 100 MWh en Australie a coûté 50 millions de dollars, soit 1,8 million de dollars pour 3.600 kWh. Et il faudra débourser cette somme tous les 10 ans, la durée de vie de cette batterie. Certaines batterie électro-chimiques ne fonctionnent pas bien quand il fait froid, d'autres ne peuvent pas être déchargées complètement. La batterie de Carnot avec pompe à chaleur n'a pas ces inconvénients.
La densité énergétique de notre batterie de Carnot est faible, 3.600 kWh / 150 m³ = 24 kWh / m³, ce qui est mieux que la densité d'un volant d'inertie (5 kWh/m³) et beaucoup mieux que l'air comprimé, mais loin derrière le lithium : 110 kWh / m³. A titre indicatif, un barrage de pompage-turbinage (STEP) a une densité de 0,12 kWh/m³.
Enogia fait partie maintenant d'un consortium européen qui va développer la batterie de Carnot avec pompe à chaleur :
On pourrait penser qu'une batterie composée d'un seul réservoir chaud chauffé par des résistances électriques, d'une turbine à vapeur et d'un aéroréfrigérant serait plus simple. Si le réservoir chaud est à 400 °C et que la turbine est refroidie à 60 °C, son rendement de Carnot, donc idéal, est de (400 - 60 ) / (400 + 273) = 0,50 auquel s'applique le rendement isentropique, soit 0,5 * 0 ,7 = 35 % de rendement réel. Ici, ce rendement isentropique ne s'applique qu'une fois, puisqu'il n'y a pas une deuxième machine, la pompe à chaleur. Un très bon aéroréfrigérant consomme 10 kW pour 170 kW de froid produits. Si on veut stocker et produire 3.600 kWh d'électricité, le froid sera 3.600 * 65 / 35 = 6.686 kWh. L'aéroréfrigérant devra donc consommer pour cela 6.686 /170 * 10 = 393 kWh. En tenant compte de cette donnée, le rendement de cette batterie SANS pompe à chaleur sera 3.600 / (3.600 +6.686+393) = 33,7 %. On voit que c'est moins que les 45 % de rendement aller-retour de la batterie de Carnot avec pompe à chaleur. De plus, l'aéroréfrigérant présente un risque de légionellose et pourrait engendrer une nuisance sonore.
Pour illustrer mon propos, voici une mini-turbine Siemens qui fonctionne dans un atelier de travail adapté en Belgique où on fabrique des palettes et qui génère de l'électricité en brûlant la sciure de bois.
Dans une toute autre échelle de grandeur, voici https://www.maltainc.com/ qui voudrait transformer les centrales au charbon en batteries de Carnot en récupérant la turbine qui servira aussi bien de turbine que de compresseur.
2. Stockage sous 100 °C.
Des réservoirs à 400 °C ne peuvent pas contenir de l'eau. Ils contiendront souvent des sels fondus qui demandent des technologies appropriées. Mais on pourrait concevoir cette batterie de façon beaucoup plus simple, sans être assujetti à de grosses contraintes techniques : prenons l'exemple d'une batterie dont la capacité de stockage est de 600 kWh, les réservoirs seront faits en béton et contiendront uniquement de l'eau. Une firme spécialisée me dit que l'eau ne peut pas être chargée en ions sulfates ou chlorures. Nos réservoirs en béton seront donc rempli d'eau de pluie et non avec de l'eau de ville. Dans le réservoir chaud, cette eau évolue entre 70 °C et 95 °C. Dans le réservoir froid, c'est de l'eau en train de congeler et de décongeler, donc un mélange d'eau et de glace qui restera constamment à 0 °C. La turbine est une turbine Enogia qui fonctionne à partir de 70 °C. Quant à la pompe à chaleur, ce sera une pompe à chaleur dite à très haute température qui existe couramment dans le commerce et qui sert à chauffer nos maisons équipées de vieux radiateurs traditionnels fonctionnant à une température de 80 °C mais, pour bien faire, la pompe à chaleur devrait pouvoir atteindre 95 °C.
Toutefois, cela conduit à une efficacité aller-retour qui n'est plus que de 20 % au lieu des 50 à 60 % si on travaille à 400 °C. C'est donc encore pire que les 25 % de l'hydrogène. Cela provient du fait que la perte isentropique s'applique à une quantité d'énergie beaucoup plus importante, puisque le rendement de Carnot de la turbine étant très faible, il faut retirer du condenseur une quantité d'énergie beaucoup plus importante. Concrètement, cette énergie se trouve dans une beaucoup plus grande masse de vapeur qui frappe les aubes des machines et la perte est donc aussi beaucoup plus importante.
Voici de façon très succincte ce que devient notre calcul.
Le rendement de Carnot est (82 °C - 0 °C) / (82 °C + 273) = 23 %
Le réservoir froid contiendra 600 kWh * 77 / 23 = 2.008 kWh
La perte isentropique de la pompe à chaleur est couverte par les panneaux solaires et cet apport est immédiatement dissipé dans la pompe à chaleur. Cette perte ne doit donc pas être stockée dans le réservoir froid.
Volume du réservoir froid : 2.008 kWh / 93 kWh/m³ de glace formée = 22 m³, soit 2,8 m * 2,8 m * 2,8 m soit une surface de 47 m²
Le réservoir chaud contiendra 2.008 + 600 = 2.608 kWh. Il doit aussi fournir la perte isentropique de la turbine. Il doit donc contenir : 2.608 * 100 / 70 = 3.728 kWh C'est ce que le réservoir chaud devra contenir.
Le volume du réservoir chaud sera : 3.728 / 1 chaleur spécifique de l'eau / 1.000 kg/m³ / (95 °C - 70 °C) * 860 kcal/kWh = 128 m³
soit 4 m * 5,6 m * 5,6 m avec une surface extérieure de 152 m²
Déperdition de chaleur du réservoir chaud en 1 mois :
152 m² * 82 °C / 1 m épaisseur laine de verre * 0,04 coefficient isolation laine de verre * 30 jours * 24 heures / 860 kcal/kWh = 418 kWh
418 kWh / 3.728 kWh = 11 % de perte de chaleur en 1 mois
Prix du réservoir chaud = 152 m² * 0,2 m béton * 500 €/m³ béton placé = 15.200 €
Prix du réservoir froid = 47 m² * 0,2 m béton * 500 €/m³ béton placé = 4.700 €
Prix isolant en laine de verre réservoir chaud = 152 m² * 1 m épaisseur * 50 €/m³ = 7.600 €
Turbine Enogia = 30.000 €
Pompe à chaleur = 20.000 €
Total 77.000 € + marge bénéficiaire = 100.000 €
La turbine Enogia coûtait à ses débuts 40.000 € mais cette firme vise un prix de 15.000 € lorsque la production aura trouvé sa vitesse de croisière.
Une batterie au lithium de même capacité de stockage de 600 kWh coûte 462.000 €. Toutefois, la durée de vie d'une batterie de Carnot avec pompe à chaleur est de 30 ans tandis que celle de la batterie au lithium est de 10 ans. Donc, sur une période de 30 ans, la batterie de lithium aura coûté 1,38 millions d'euros tandis que la batterie de Carnot aura coûté 100.000 €
Comparons la batterie de 3.600 kWh contenant de l'eau avec celle contenant le basalte. Le réservoir chaud contenant de l'eau aura un volume de 770 m³, soit 7 m haut * 10 m large * 10 m haut tandis que celui qui contient le basalte aura un volume de 92 m³, soit 4,5 m haut * 4,5 large * 4,5 long. Le réservoir du basalte est significativement plus petit que celui de l'eau, mais quand on regarde les dimensions linéaires, la différence n'est plus aussi impressionnante, avec comme avantage de l'eau de pluie d'être gratuite alors qu'il y a des tonnes de basalte qu'il faut payer..Par contre, le réservoir du basalte en acier coûte moins cher que celui en béton du fait de sa plus petite taille. Finalement, le réservoir chaud coûte la même chose, qu'il contienne de l'eau ou du basalte.
****************************************************
Le texte ci-dessus décrivait la batterie de Carnot avec pompe à chaleur qui pourrait être bien utile aux éleveurs ayant besoin de beaucoup de chaleur pour leurs jeunes animaux. Il y a peut-être une autre solution moins sophistiquée : le réservoir d'eau chaude.
En effet, on peut imaginer stocker l'énergie des panneaux solaires dans de grands réservoirs remplis d'eau dont la température évolue entre 60 et 95 °C. Ils seront chauffés par des résistances électriques alimentées par les panneaux solaires. Ces températures sont couramment utilisées pour alimenter les radiateurs que nous avons dans nos maisons. On ne peut pas monter au-dessus de 95 °C, car l'eau va se mettre à bouillir et former de la vapeur, ce qui va créer des pressions très dangereuses.
Pour qu'un mètre cube d'eau voie sa température monter de 60 à 95 °C, il doit recevoir 1.000 kg/m³ * 1 chaleur spécifique de l'eau * (95 °C - 60 °C) / 860 kcal/kWh = 40 kWh/m³.
Un élevage de poulets nécessite 15 kWh/m².an . On peut tenir 10 poulets au mètre carré. Un élevage de 40.000 poulets demandera donc 15 kWh/m² * 40.000 poulets / 10 poulets/m² = 60.000 kWh/an. Un mètre carré de panneaux photovoltaïques produit 200 kWh/m².an. Pour couvrir tous ses besoins en énergie, cet élevage de 40.000 poulets devra être couvert de 60.000 kWh / 200 kWh/m² produits par les panneaux photovoltaïques = 300 m² de panneaux photovoltaïques.
On pourrait facilement chauffer ce poulailler industriel avec des ventilo-convecteurs, contrairement à un élevage de porcs où la chaleur est surtout destinée aux porcelets et non à la mère, ce qui compliquerait l'aménagement du bâtiment et rendrait l'installation très coûteuse. Mais on peut imaginer un chauffage par le sol pour les porcelets avec un ventilo-convecteur mettant l'ambiance à une température acceptable aussi bien pour la mère que pour les jeunes.
Revenons à nos poulets. En moyenne, cet élevage nécessitera 60.000 kWh/an / 365 jours = 164 kWh par jour, moitié pendant la journée, moitié la nuit. La nuit, l'élevage aura besoin donc d'environ 82 kWh. Or, un mètre cube d'eau peut stocker 40 kWh/m³. Avec 2 m³, nous aurions suffisamment pour chauffer le poulailler la nuit. Cela semble très peu. Toutefois, les panneaux solaires ne fonctionnent pas quand il n'y a pas de soleil. Il faudrait donc pouvoir stocker pour une ou deux semaines. Un réservoir de 120 m³ pourrait donc fournir la chaleur jour et nuit pendant 30 jours. Ce système semble donc très économique et permettra d'économiser 60.000 kWh * 0,43 €/kWh électricité, soit 26.000 € par an. Il faudra affiner ce calcul, car cet élevage n'a pas besoin de la même chaleur tout au long de l'année.
D'après un étude française, une truie a besoin de 983 kWh/an. Pour un élevage de 1.000 truies, il faudrait 1.000.000 kWh / 365 jours = 2.800 kWh/jour qui pourraient être stockés dans 2.800 kWh / 40 kWh/m³ = 70 m³, ce qui n'est pas beaucoup vu l'ampleur de cet élevage. Si on veut stocker la chaleur pour 15 jours, il faudrait un réservoir de 1.000 m³ et faire des aménagements importants dans le bâtiment pour distribuer la chaleur. Mais comme cet élevage dépense actuellement 430.000 €/an pour les lampes à infrarouges, je crois que le jeu en vaut la chandelle.
Si l'éleveur de poulets ne possède pas de panneaux photovoltaïques, il devra acheter 300 m² panneaux solaires au prix de 300 €/m² de panneau = 90.000 €. S'il dispose de panneaux solaires, et si nous voulons que le réservoir et ses ventilo-convecteurs soient amortis en six ans, il faudrait que l'installation ne coûte pas plus de 6 * 430.000 € = 2.500.000 € pour les porcs et 6 * 26.000 € = 150.000 € pour les poulets. Cela semble réaliste.
Au vu de la quantité d'énergie consommée, le besoin de la stocker apparaît plus aigu en élevage porcin.
L'avantage de l'eau comme moyen de stockage de la chaleur est qu'elle peut contenir énormément de chaleur pour un volume donné, bien plus que les autres matières. Malheureusement, la température ne peut pas dépasser 100 °C, sinon de la vapeur va se former et créer de très fortes pressions, ce qui est extrêmement dangereux. Mais on pourrait remplacer l'eau par du basalte et monter nettement en température. Cela permettrait par exemple à une boulangerie de chauffer ses fours à 180 °C à partir de basalte porté à 400 °C par des résistances électriques alimentées par des panneaux photovoltaïques.
****************************************************
De la même façon, on peut imaginer stocker du froid pour conserver des fruits, comme les poires par exemple, ou encore les pommes de terre.
Un congélateur refroidit un réservoir contenant de l'eau glycolée afin que celle-ci puisse rester liquide quand elle atteindra -25 °C. Cela ne signifie pas qu'il y aura -25 °C dans la chambre froide. Simplement, on va prélever un peu de ce froid extrême pour le diluer dans la chambre froide qui sera ainsi maintenue à par exemple +5 °C. On pourrait aussi congeler de l'eau pure, en bénéficiant alors d'un changement de phase, puisque former de la glace demande beaucoup d'énergie. Cela réduirait le volume du réservoir. Cependant, la glace est un bon isolant et récupérer le froid ne serait pas facile.
Si la chaleur extraite de la chambre froide est de 2 kWh, l'électricité consommée par le compresseur de son groupe frigorigène est généralement de 1 kWh. Cela conduit à un coefficient de performance (COP) de 3, une valeur habituellement rencontrée. Cela signifie, qu'avec par exemple 60.000 kWh d'électricité produits par an par les panneaux solaires, on peut stocker 120.000 kWh dans un réservoir très bien isolé, dans lequel ce froid peut être conservé des mois si le réservoir est suffisamment grand (les petits réservoirs perdent toute leur chaleur en peu de temps). L'isolant est ce qui coûte le plus cher dans ce genre de réservoir thermique, mais on peut remplacer la laine de roche (coefficient d'isolation 0,04) par de la paille (coefficient 0,05 , donc très voisin). La paille est compatible avec les températures envisagées et coûte 16 fois moins que la laine de roche. En parlant d'isolation, je me demande si on ne pourrait pas isoler les murs du hangar en empilant simplement de grandes balles carrées de paille le long de ces murs. Ce doit être efficace pour un coût peu élevé étant donné les dimensions de ces ballots. On perd simplement un peu de place. Reste alors à isoler le sol et le toit du hangar.
Le fait que le réservoir soit très grand est un avantage : il permet de conserver le froid très longtemps, et ainsi de stocker le froid avec les panneaux solaires en été, lorsqu'il y a beaucoup de soleil, et de pouvoir bénéficier de la réfrigération en hiver quand le soleil se fait rare. On peut toutefois se demander si autant de froid est encore nécessaire en hiver, alors qu'il y a + 5 °C à l'extérieur, ce qui est plus ou moins la température dans la chambre froide. Ce n'en est que plus favorable, puisqu'en hiver les panneaux solaires donnent peu.
On voit donc que conserver le froid sur une aussi longue période est inutile. Je lis sur internet qu'un entrepôt frigorifique consomme 400 kWh/m² et par an. Supposons que le hangar réfrigéré ait une superficie de 1.000 m². Par an, il devrait donc consommer 400.000 kWh/an, principalement en été. Par jour d'été, la réfrigération consomme donc environ 400.000 kWh / 200 jours = 2.000 kWh / jour. Comme un mètre carré de panneau solaire produit environ 1 kWh/jour, 2.000 m² de panneaux (20 ares) seraient nécessaires. Il n'y a pas du soleil tous les jours en été. Ils faudrait donc pouvoir stocker le froid pendant une certaine période, mettons 30 jours, ce qui semble suffisant pour avoir un changement de temps et retrouver le soleil après de nombreux jours pluvieux. Le réservoir contenant le froid doit donc pouvoir stocker 2.000 kWh/jour * 30 jours = 60.000 kWh.
En réalité, les panneaux photovoltaïques permettent de bénéficier d'une autoconsommation de 1/3. Cela veut dire que nous pourrons utiliser directement l'électricité produite par les panneaux solaires sans devoir stocker pendant 1/3 du temps. Les 2/3 restants, la nuit notamment, nous devrons utiliser la chaleur stockée. Il faudra donc stocker 2/3 * 2.000 kWh/jour = 1.333 kWh et pour couvrir 30 jours, la capacité du réservoir devra donc être de 40.000 kWh.
Quel est le volume de ce réservoir ? La chaleur spécifique de l'eau glycolée est de 0,88. Nous utilisons la formule : chaleur stockée = masse * chaleur spécifique * écart de température. Si l'eau glycolée évolue de -25 °C à 0 °C et qu'il faut stocker 40.000 kWh, le volume du réservoir sera : 40.000 kWh / 25 °C / 1.000 kg/m³ eau glycolée / 0,88 chaleur spécifique eau glycolée * 860 kcal/kWh = 1.500 m³, soit un réservoir de 5 m haut * 17 m large * 17 m long.
Si le réservoir contient de l'eau pure qui est congelée et donc devient de la glace en passant de +5°C à - 5 °C, un mètre cube contiendra 1.000 kg eau * 80 kcal/kg chaleur fusion de la glace / 860 kcal/kWh + 1.000 kg eau * 1 chaleur spécifique de l'eau * (5 °C - -5 °C) / 860 kcal/kWh = 104 kWh/m³. Le volume du réservoir sera alors de 40.000 kWh / 104 kWh/m³ = 384 m³, soit quatre fois plus petit qu'avec l'eau glycolée. Toutefois, cette eau glycolée peut facilement être pompée et passer dans des échangeurs de chaleur, tandis que la glace nécessite probablement la construction de serpentins dans lesquels circulera un autre fluide. De plus, la formation de glace s'accompagne d'une augmentation du volume, ce qui peut créer des contraintes mécaniques sur les parois du réservoir.
Si le réservoir de 1.500 m³ est isolé avec une épaisseur de 1 mètre de paille, on peut calculer la perte de chaleur suivant la formule :
Déperditions = surface extérieure du réservoir * écart de température avec l'extérieur / épaisseur isolant * coefficient isolation paille * durée.
En été, le réservoir aura une température moyenne de (0 °C + -25 °C) / 2 = -12,5 °C tandis qu'à l'extérieur, il y a une moyenne jour-nuit de 20 °C, ce qui fait un écart de 32,5 °C. La surface du réservoir est de 900 m².
Dans notre exemple, et pour une durée de stockage de 1 mois d'été, la perte sera :
Déperditions = 900 m² * 32,5°C écart moyen / 1 m paille * 0,05 coefficient isolation paille * 1 mois * 30 jours/mois * 24 heures/jours / 860 kcal/kWh = 1.224 kWh, alors que le réservoir contient 40.000 kWh. Donc, après 1 mois d'été, la perte est de 1.224 / 40.000 = 3 %.
Cette solution paraît donc très intéressante, mais pourrait se révéler irréaliste si son prix est beaucoup trop élevé. Le réservoir devrait coûter fort cher à la construction. S'il est construit en acier, celui-ci coûterait, rien que pour les matériaux, 900 m² * 0.015 m épaisseur acier avec profilés * 7.000 kg acier/m³ * 1,5 €/kg acier = 140.000 € auxquels il faut ajouter la main d'oeuvre et le bénéfice du patron. Il faut aussi ajouter le prix du congélateur et des panneaux solaires, mais cela devrait permettre d'économiser 400.000 kWh * 0.43 €/kWh = 172.000 €/an. Les réservoirs en acier semblent donc coûter fort cher. Des réservoirs en béton devraient être plus abordables.
Si les parois du réservoir sont faites en béton et ont une épaisseur de 20 cm, le volume de béton serait de 900 m² * 0,2 m = 180 m³ et si le béton armé coûte 500 €/m³ placement compris, le réservoir coûterait 90.000 €, auxquels il faut ajouter les panneaux photovoltaïques à raison de 300 €/m², soit 2/3 autoconsommation * 2.000 m² * 300 €/m² = 400.000 € ainsi que le congélateur. On voit donc que ce n'est pas le réservoir de froid qui coûte le plus.
Il faudrait savoir exactement combien un entrepôt de fruits consomme de kWh par an, car les chiffres cités ci-dessus ne sont que des estimations, voire des suppositions. Les agriculteurs pourront refaire les calculs en tenant compte de leur réalité, notamment de la consommation réelle des espaces réfrigérés qu'ils ont.